A Guide to Neural Radiance Fields

A simple guide to help understand and implement Neural Radiance Fields

Written by Daniel Song

Posted on December 17, 2024

Preface

This guide provides an overview of how Neural Radiance Fields (NeRF) work, aiming to replicate the results from the original paper. It is divided into six parts, each explaining the implementation of different aspects of NeRF using PyTorch. A basic understanding of neural networks is assumed; for those who need a refresher, the 3Blue1Brown video linked here may be helpful. Links to Google Colab notebooks are included as templates to follow along with the material.

**Side note: I wrote this guide during the summer after my junior year of undergrad as a personal project, following my professor’s suggestion. I decided to post this online to hopefully help others who may also want to reimplement the paper.**

An example of a rendered output using NeRF. Source: Mildenhall, et al., 2020 [1]

What Are NeRFs?

A Neural Radiance Field (NeRF) is a method to generate novel views of a scene or object in a 3-dimensional space, trained from a set of 2-dimensional images and their corresponding poses (position and direction). NeRFs could be thought of as a method of 3D scene reconstruction, in which we can render new views of the scene from different positions and directions. When NeRFs were introduced, it was highly regarded due to their ability to create high-quality photorealistic 3D reconstructions.

Source: Mildenhall et al., 2020 [1]

Why Use NeRFs?

Most methods of representing 3-dimensional scenes use a discrete set of values representing polygons such as triangles (commonly known as a mesh), or by using voxels (a 3D counterpart to a pixel). NeRFs, however, can represent the scene as a continuous function. This enables a much more detailed representation of the scene without being limited to the “resolution” of voxels or the number of triangles. Furthermore, NeRFs are often more compact than meshes or voxels, using much less memory as the weights of the model are all that are needed to represent a certain scene. The original implementation “requires only 5 MB for the network weights (a relative compression of 3000× compared to LLFF), which is even less memory than the input images alone for a single scene from any of our datasets” (Mildenhall et al.).

How Does It Work?

At its core, the main model for NeRF is quite simple. It is a multilayer perceptron consisting of 8 fully connected layers, each with 256 channels. The model takes a position in space and a viewing direction as input and outputs a color and density value. Using this, we can sample many colors and densities from the network to generate a final image. The idea is to shoot out many rays from the camera, one ray for each pixel in the output image. For each ray, we sample points along the ray to retrieve their colors and densities. These values are then integrated along the ray to calculate the final pixel color value.

Source: Mildenhall et al., 2020 [1]

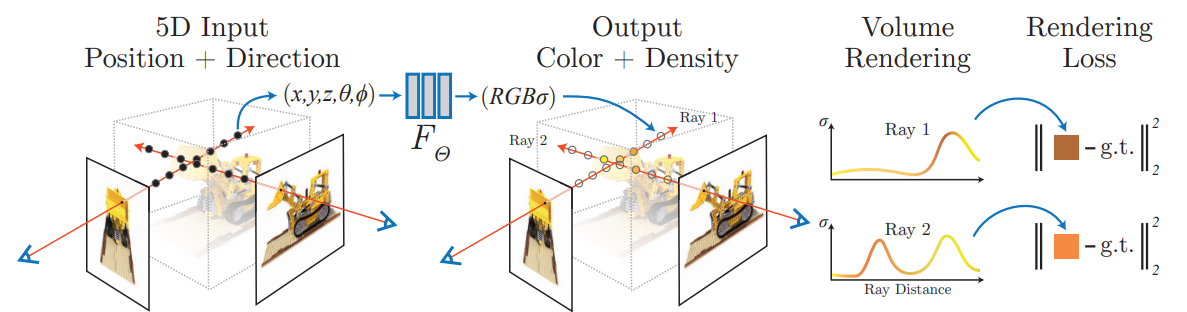
This volume rendering technique is differentiable, meaning that we can optimize it. We can create a rendering loss function with respect to the ground truth image and train the model.

Now let’s try to make our own implementation of NeRFs!

Part 0: Setup

This section will go over setting up the environment so that you can follow along with the guide below. There will be multiple Jupyter notebooks to serve as templates for working along with the guide.

There are two main ways you may use the Jupyter notebooks which depends on whether or not you have a CUDA-compatible machine.

Using Your Own Machine

If you have an Nvidia graphics card that supports CUDA (e.g. RTX 30 series, 40 series), and has at least 8GB of VRAM, then it might be better to use your own machine, as the free machines available through services such as Google Colab are often less powerful. Make sure you are able to use CUDA, which you can set up through this guide from Nvidia.

It is recommended to use a package manager such as Conda to easily download and install the required libraries (PyTorch, NumPy, Matplotlib, tqdm, opencv-python).

Using Online Services

If you do not have a capable graphics card, you may use online services such as Google Colab or Kaggle. These services usually allow you to import a notebook and run the code immediately. The free versions of these services often have GPUs that are not as powerful, so if you want to reduce the training time or prevent getting kicked out after inactivity, using paid GPU rental services like Lambda Labs may also be helpful. However, I would recommend first working through this guide with free services or your own machine to make sure they work, before actually training the neural network.

Part 1: Preparing the Input Data

The Jupyter Notebook for this section can be found here.

Creating the Rays

Before creating the neural network of the model, we first need to prepare the input data into a format that the neural network can work with. We know that the model takes in a position and direction, and outputs a color and density value. But to get the positions, we need the rays for each pixel that we are going to eventually output so we can later sample points along this ray for the positions.

Image created by Daniel Song

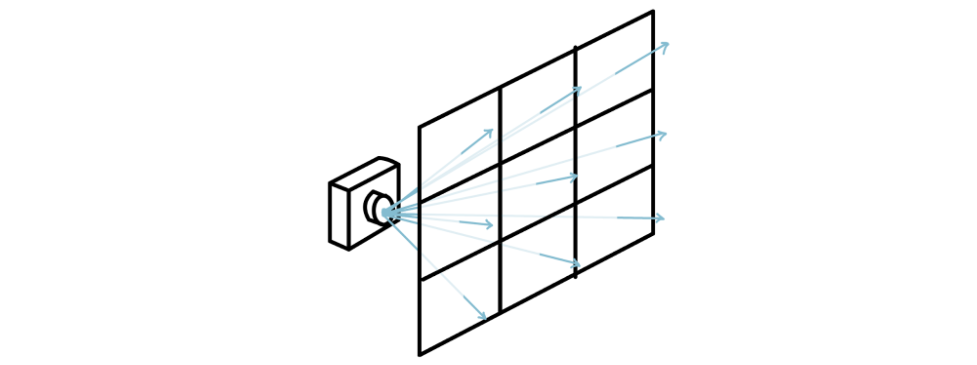
Let’s start by understanding the math behind calculating the rays. We want to know a point(origin) and a direction to represent a ray in the real-world coordinate system. This is to represent the ray that originates from the camera, passes through the pixel we want to output, and will hopefully pass through the object in question. What information do we have? We have the set of images, but we also have the camera pose. This is often represented as a matrix and is the key information we need. For the dataset used in this guide (along with most implementations of NeRFs), we are provided with the camera-to-world transformation matrix. A camera-to-world transformation matrix looks something like this:

\[\begin{bmatrix} R_{00} & R_{01} & R_{02} & t_x \\ R_{10} & R_{11} & R_{12} & t_y \\ R_{20} & R_{21} & R_{22} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

where the 3x3 matrix \(\boldsymbol{R}\) represents the orientation (rotation) of the camera, and \(t\) represents the translation of the camera. Using this matrix, one could transform a point in the camera coordinate system to the “real world” (not really the true real world, but more of an estimate of the positions relative to each image given).

Now let’s try to calculate the origin and direction of all the rays. Calculating the origin is fairly simple. This is simply the \(t\) of the camera, given in the matrix (all rays for a particular output image will have a single origin).

To get the directions, we will first create a grid of homogeneous directions in the camera space. Using PyTorch’s meshgrid allows us to create a grid of coordinates, which we will translate to the left and up so that the center of the grid has the coordinates of 0, 0. Then, to convert this into homogenous directions, we will divide this coordinate grid by the focal length. These will become the \(x\) and \(y\) coordinates of the direction vectors, and we will set the \(z\) coordinate to be \(-1\). We now want to convert this into the world space by multiplying these vectors by \(\boldsymbol{R}\). In short, the direction vectors will be defined as follows, where \(W\) and \(H\) are the width and height, \(i\) and \(j\) are coordinates on the original meshgrid, and \(f\) is the focal length of the camera:

\[\mathbf{o} = \begin{bmatrix} R_{00} & R_{01} & R_{02} \\ R_{10} & R_{11} & R_{12} \\ R_{20} & R_{21} & R_{22} \end{bmatrix} \begin{pmatrix} \frac{i - \frac{W}{2}}{f} \\ -\left( \frac{j - \frac{H}{2}}{f} \right) \\ -1 \end{pmatrix}\]

You may have noticed that the \(y\) axis is multiplied by \(-1\). This is because, in the image coordinate space, the \(y\) indexing works from top to bottom (increases as you go downwards), whereas the real world works the other way around. So, we multiply it by \(-1\) to compensate.

As a result, we now have \(W\cdot H\) homogeneous rays in the camera space pointing toward each of the pixels.

We also want to expand the ray origins to match the shape of the directions, so that we have the same number of origins as directions.

NDC Rays

Although using the rays we calculated so far works well enough for a synthetic dataset (e.g. a model or scene rendered through something like Blender), the authors also convert these rays into the normalized device coordinate (NDC) space for real images. In the authors’ words: “ This space is convenient because it preserves parallel lines while converting the z-axis (camera axis) to be linear in disparity” (Mildenhall et al.).

The equation below defines the projection of the rays that we had into the NDC space.

\[\mathbf{o}' = \begin{pmatrix} -\frac{f}{W/2} \frac{o_x}{o_z} \\ -\frac{f}{H/2} \frac{o_y}{o_z} \\ 1 + \frac{2n}{o_z} \end{pmatrix} \quad \mathbf{d}' = \begin{pmatrix} -\frac{f}{W/2} \left( \frac{d_x}{d_z} - \frac{o_x}{o_z} \right) \\ -\frac{f}{H/2} \left( \frac{d_y}{d_z} - \frac{o_y}{o_z} \right) \\ -2n \frac{1}{o_z} \end{pmatrix}\]

The derivation behind this can be found in the appendix (pp. 19-22) of the original paper.

Implementing this projection should be fairly straightforward as it is a function that modifies the given ray origin and directions.

Sampling

Now that we have the rays, we have to sample positions along the ray so we can feed them into the neural network. Here, we will be doing something called stratified sampling. Stratified sampling is a sampling technique where we divide the population into smaller groups and then sample from each of them. In this case, we will be dividing the ray into \(N\) equally sized bins, and draw one uniformly random sample from each of the bins like such:

\[t_i \sim \mathcal{U} \left[ t_n + \frac{i-1}{N} (t_f - t_n), \, t_n + \frac{i}{N} (t_f - t_n) \right]\]

Here, \(i\) is the index of the sample from \(1 \ldots N\), and \([t_n,t_f]\) represents the beginning and end of the ray.

You may be wondering, why not just sample uniformly along the ray, each point equidistant to each other? This is because this approach would limit the representations’ quality and resolution, because “the MLP would only be queried at a fixed discrete set of locations” (Mildenhall et al.). The stratified sampling approach would effectively help the neural network learn a continuous representation of the scene or object.

Implementation-wise, we are going to do things a bit differently so we can utilize vectorized operations from the torch library to its fullest. We are first going to define z_vals (which will later represent the integration time of the points along the ray) to be \(N\) equally spaced values on the range of [near, far].

Now to implement the actual sampling process, we’re going to define the upper and lower bounds of each group, where upper[i] and lower[i] represent the bounds of the ith group. We will start by calculating the middle values of z_vals by averaging the adjacent values in z_vals. (i.e. average z_vals[1:] and z_vals[:-1]). Next, if we concatenate the first value of z_vals to the front of mids, then it becomes the lower bounds, whereas if we concatenate the last value of z_vals to the end of mids, then this list becomes the upper bounds. We can then generate \(N\) random numbers in the range of [0,1), and now, if we just add the width of the group scaled by these random values to the lower bounds, we have the stratified sampled distances

The final step is to calculate the actual points, which is done by adding the scaled ray directions (using z_vals) to the ray origins.

def stratified_sampling(rays_o, rays_d, near, far, n_samples):
  z_vals = torch.linspace( ... , device=rays_o.device) # TODO

  mids = ... # TODO
  lower = ... # TODO
  upper = ... # TODO

  rands = torch.rand([n_samples], device=z_vals.device)

  z_vals = lower + (upper - lower) * rands

  z_vals = z_vals.expand(list(rays_o.shape[:-1]) + [n_samples])

  pts = ... # TODO
  return pts, z_vals

You may notice here that we are outputting not only the points along the ray but also z_vals. Like mentioned above, this represents the integration time of the points along the ray, which will be useful for the volume rendering integration later.

Positional Encoding

Using the positions and directions directly produces a low-fidelity result, as it is difficult for a network to directly predict high-frequency values from a low dimensional domain (our positions and directions), so the authors of the paper found that using Fourier features greatly improves the results, found in this paper. Here is a 3-minute video by the author that explains it very well. In a nutshell, we are encoding the position and direction vectors into higher-dimensional vectors, which capture more detailed spatial information and make it easier for the model to learn complex functions.

Source: Mildenhall, et al., 2020 [1]

Though the paper mentions three different methods of mappings (basic, positional, and Gaussian), the NeRF paper uses a slightly modified version of the positional encoding method defined as the following:

\[\gamma(p) = \left( \sin(2^0 \pi p), \cos(2^0 \pi p), \dots, \sin(2^{L-1} \pi p), \cos(2^{L-1} \pi p) \right)\]

where \(p\) represents the input vector (in our case, the position and direction), and \(L\) represents the number of frequency functions we want to use. One way to implement this encoder is to create a list of alternating lambda functions that apply either the \(\sin\) or \(\cos\) function. We will also keep the original input values, leading to a total output dimension of \(I(1+2L)\) where \(I\) represents the input dimension. We will also be omitting the \(\pi\) coefficients for the actual implementation. The reasoning behind this is given by the author here.

class PositionalEncoder():
  def __init__(self, input_dim, n_freqs):
    self.input_dim = input_dim
    self.n_freqs = n_freqs
    self.output_dim = input_dim * (1 + 2 * self.n_freqs)
    self.gamma = [lambda x: x]

    ... # TODO

  def encode(self, x):
    return ... #TODO

The code above provides a template for the Encoder class. Here, we have a list, gamma, that represents the \(\gamma\) function. Implement the rest of the constructor and encode function to implement the positional encoder. You may assume that the parameter x for the encode function is of shape (..., input_dim).

Part 2: Creating the Model

The Jupyter Notebook for this section can be found here.

As mentioned before, the model itself is a relatively simple neural network. Let’s try to implement the model. The paper provides a diagram of the neural network, which is shown below.

Source: Mildenhall, et al., 2020 [1]

As explained in the paper, “all layers are standard fully-connected layers, black arrows indicate layers with ReLU activations, orange arrows indicate layers with no activation, dashed black arrows indicate layers with sigmoid activation, and “+” denotes vector concatenation” (Mildenhall et al.). The model takes in a position \(\mathbf{x}\) and a viewing direction \(\mathbf{d}\) and outputs a total of four values for the RGB and \(\sigma\) values. The green blocks with the gamma function represent the 60-dimensional vector output of the positional encoding functions.

This can all be represented as a single class using PyTorch’s nn.Module. For those who haven’t worked with PyTorch before, this short tutorial may be helpful.

For the implementation, we’re going to have several parameters to improve the customizability of the network. The pos_dim and dir_dim parameters will be the dimensions of the input position and direction vectors, whereas the hidden_dim will be the channel sizes of the hidden layers.

To make the forward method simpler, we can group the layers into blocks. The first block will consist of the first four linear layers of hidden_dim channels, applying the ReLU activation function after each linear layer. We can have a second block that is similar to the first block, except that the first linear layer’s input channel dimension will instead be hidden_dim + pos_dim to account for the concatenated input vector. Next, we can have a separate layer defined for outputting the predicted density as a linear layer with an output dimension of 1 (alpha_out). For predicting the RGB values, we will need a few more separate layers. We want to pass the values into another linear layer of 256 channels (features_linear), then a linear layer with an input dimension of hidden_dim + dir_dim (for the concatenated viewing direction) and an output dimension of hidden_dim // 2 (views_linear), a ReLU activation function, and a final layer that converts the hidden_dim // 2 vector into RGB values (output_linear).

class NeRFModel(nn.Module):
  def __init__(self, input_dim=3, input_dim_dir=3, hidden_dim=256):
    super(NeRFModel, self).__init__()

    self.block1 = nn.Sequential(...) # TODO
    self.block2 = nn.Sequential(...) # TODO

    self.density_out = ... # TODO
    self.rgb_filters = ... # TODO
    self.branch = ... # TODO
    self.output = ... # TODO

    self.input_dim = input_dim
    self.input_dim_dir = input_dim_dir
    self.relu = nn.ReLU()

  def forward(self, x):
    ... # TODO

The general flow of the network follows the diagram explained above, but there is a slight detail in implementing the final RGB calculation that is not mentioned in the diagram. To start from the beginning, we have an input position (that may not necessarily be 3 dimensional due to the positional encoding) that is passed through the first block. We then concatenate the original input positions onto this output and pass this through the second block. Then to predict the density, we pass the output to alpha_out. Separately, to predict the RGB values, we first pass the output from the second block to features_linear, then concatenate the viewing directions before passing it through views_linear, then finally passing it to the output_linear.

Part 3: Model Outputs to Image

The Jupyter Notebook for this section can be found here.

Now that we have the inputs and the model, it is time to convert the model outputs into an image. The goal is for each ray, to combine all the colors and density values to calculate a final output pixel color. For this function, we will need the raw outputs from the model, z_vals from the sampling method, and rays_d for the directions of the rays. The equation that will be used to calculate the color is derived from the volume rendering equation (Eqn. 1 in the paper), to be rewritten and estimated as a weighted sum of the sampled colors along the ray like such:

\[\hat{C}_c(\mathbf{r}) = \sum_{i=1}^{N_c} w_i c_i, \quad w_i = T_i \alpha_i, \quad \alpha_i = \left( 1 - \exp(-\sigma_i \delta_i) \right),\] \[\begin{aligned} T_i &= \exp \left( -\sum_{j=1}^{i-1} \sigma_j \delta_j \right) \\ &= \prod_{j=1}^{i-1} \exp(-\sigma_j \delta_j) \\ &= \prod_{j=1}^{i-1} (1 - \alpha_j) \end{aligned}\]

where \(c_i\) and \(\sigma_i\) are the colors and densities along the ray \(\mathbf{r}\), and \(\delta_i=t_{i+1}-t_i\) is the distance between adjacent samples.

As you can see, there are multiple parts to this equation. The easiest way to implement this would be to work backward, starting by defining the \(\delta\) values. This can be done by calculating the difference between consecutive elements of z_vals and then multiplying each distance by the corresponding normalized directions. Then, we can calculate the \(\alpha\) values by using the equation stated above. However, to introduce non-linearity, the \(\sigma\) values should be passed through the ReLU function.

To calculate the weights, the easiest way would be to use the cumprod function with the exclusive flag. Since PyTorch does not have the exclusive flag, I have defined a function to mimic the behavior in the notebook.

Now all that is left is to calculate the rgb_map by calculating the sum of the rgb values multiplied by the weights along each ray. Again, before we do this, we will pass the raw values through an activation function (this time, the sigmoid function) to introduce non-linearity.

Part 4: Hierarchical Sampling

The Jupyter Notebook for this section can be found here.

Currently, we are using a stratified sampling method for each ray. However, many parts of the ray may be either empty or occluded, leading to many of the sampled points not contributing as much to the final rendered image. The way the authors work around this problem is to actually train two networks at the same time: one “coarse” model and another separate “fine” model (which will have the same network structure as the coarse). The coarse model will work the same way we have implemented so far. However, the fine model will use a different sampling approach, where samples are more concentrated towards the relevant parts of the scene.

In Part 3, we converted the model outputs to a pixel color value using a sum of weighted color values. You may remember that we also had the weights as part of the output of the function. This is because we can normalize these weights to create a probability density function (PDF) which allows us to bias our sampling method towards the more relevant parts of the scene. To achieve this, we first convert this PDF to a cumulative density function (CDF) by using PyTorch’s cumsum function. In order to take samples from this CDF, we first need to generate a set of sample points \(u\) that correspond to the range of the CDF (0 to 1). The sample points are drawn randomly, introducing stochasticity to the sampling process, which can improve the model’s ability to generalize by preventing overfitting to specific regions along the ray.

Now that we have the sampled points , the next step is to determine where each of the points lies in the domain of the CDF. However, since our CDF is defined by a discrete set of points, we can first use PyTorch’s searchsorted function to determine the closest pair indices just above and below the sample point in the CDF. With these indices, we then gather corresponding values from the CDF and the original bin centers (the z_vals from the stratified sampling). We can now interpolate between the bin centers using the values of the CDF. This whole process allows us to convert a uniformly random sample of points into a random sample following the distribution defined by the original PDF.

Image created by Daniel Song

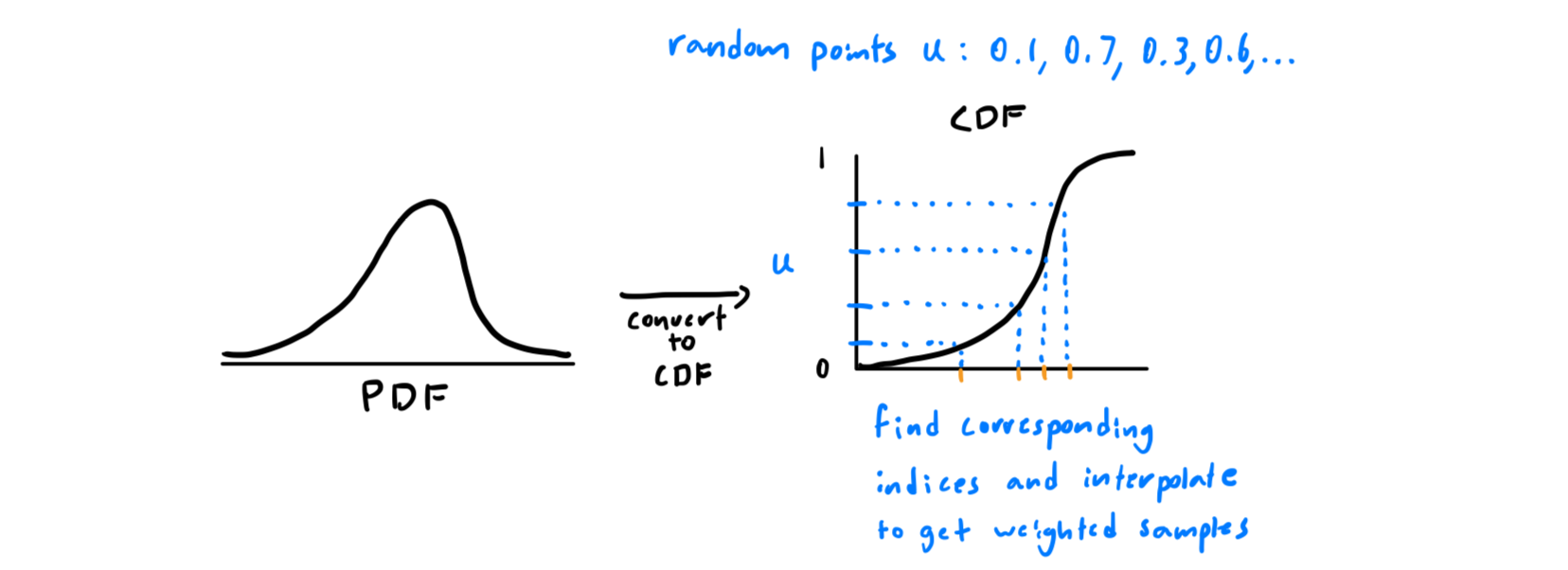
Now that we have the new z_vals, we can combine these z_vals with the old stratified sampled z_vals and calculate the final points along the ray by adding the scaled directions to the ray origins.

Part 5: Training the Model

The Jupyter Notebook for this section can be found here.

Now it is time to train our model! Training our NeRF model involves many steps and will combine everything that we have worked on so far. The Jupyter Notebook contains a skeleton for a class that will handle the training process of the neural networks that we created. There are many parameters that we can tweak, which are listed as the class instance variables. There are also many helper methods that I have already defined, but the most important ones are the forward, and the training methods.

The Forward Method

Let’s first start with the forward method. This method will define the overall forward process of passing data to the network and retrieving the results, converting them to final RGB values. The main input to this method will be the rays. First, we want to apply stratified sampling on the rays to get the query points and z_vals for the coarse network. We also want to normalize the ray directions before passing them to the network. The next step is to pass these query points and view directions to the positional encoders to get the embedded positions and directions. We can then concatenate the positions and directions along the last dimension to prepare them for the neural networks.

You may have noticed that I use the batchify method. This method is just a way to prevent out-of-memory errors by passing the input data into the neural network in chunks and then combining the outputs together. Note that this is different from the traditional random batching in gradient descent, as it is simply just a way to split an already given batch into smaller chunks to make it easier to work with. This enables us to use larger actual random batches during training without needing to worry about memory issues.

Once we get the raw outputs from the coarse model, we can reshape the raw outputs and pass them through the raw2outputs method we created earlier to get the RGB map and weights. Now, if we are using a hierarchical sampling approach, we can repeat this whole process, except this time, we are using the sample_hierarchical method, along with the output weights and z_vals from the coarse outputs.

The Training Loop

With the forward method defined, we can move on to the actual training loop!

The overall process of the training loop is to randomly grab a batch of input data, feed it forward to the network, calculate the loss, perform gradient descent, and then repeat this process over and over until the loss converges. To grab the random batch, we will be using two different strategies. One is to simply shuffle all the rays from our training dataset and grab a certain number of rays for each iteration. The other method is to randomly select an image and grab a portion of rays from the image.

The reason for these two methods is because of the different approaches to training the network for a synthetic dataset and a real-world dataset. For synthetic datasets, a large portion of the image is often blank, meaning that most of the rays that we will grab are also going to have blank color values. This hinders the training process of the network, as it will often find bad local minimums, preventing it from properly converging. What we will do instead is to grab a random image, and for the first few hundred iterations, crop the center of the image out, and then grab some rays to ensure that we have properly colored rays to minimize the chance of the network finding a bad local minimum. For real-world datasets, we do not have this issue, so we can simply just shuffle the rays and grab batches from them.

Once we have the rays, either through an image selection or a random shuffled batch, we can now pass these to the forward method we defined earlier. This gives us the RGB values of the coarse model and the fine model. Now we have to define the loss function. The paper uses the following loss function:

\[\mathcal{L} = \sum_{\mathbf{r} \in \mathcal{R}} \left[ \left\| \hat{C}_c(\mathbf{r}) - C(\mathbf{r}) \right\|_2^2 + \left\| \hat{C}_f(\mathbf{r}) - C(\mathbf{r}) \right\|_2^2 \right]\]

“where \(\mathcal{R}\) is the set of rays in each batch, and \(C(\mathbf{r})\), \(\hat{C}_c(\mathbf{r})\), and \(\hat{C}_f(\mathbf{r})\) are the ground truth, coarse volume predicted, and fine volume predicted RGB colors for ray \(\mathbf{r}\) respectively” (Mildenhall et al.).

This equation simply means that we will use a sum of the mean squared error losses of the coarse and fine model.

Now that we have the loss defined, all that is left is to perform gradient descent and run the network on a validation set periodically.

Using a Dataset

Now that we have defined the NeRF training process, it is time to use a dataset to train the model. For this section, I have prepared scaled versions of the original Lego dataset from the paper here (the number after the dataset name represents the scaling factor that was applied). These datasets are just pickled files created using NumPy that you can load using NumPy’s load function.

The file contains key-value pairs, among which we will use the images, poses, i_train, i_test, and hwf keys to retrieve the image RGB values, their corresponding poses as a matrix, the indices of the train and test, and a tuple of the Height Width Focal (HWF) values respectively. To prepare this dataset into workable rays, we will be using the get_rays and rays_to_NDC functions that we wrote before.

There are synthetic datasets and real-life datasets, each having slightly different arguments that we want to use for training. As mentioned above, there are many arguments that we have control over. Here are the most important ones explained:

The following lists the arguments used in the original paper for a synthetic dataset:

The following lists the arguments used in the original paper for a real-life dataset:

Tips for Training

Below are some tips for training.

Part 6: Custom Datasets

One of the most exciting parts of this project is to use our own videos to train the network. However, one of the most important aspects of creating a dataset is that a model will only ever be as good as the dataset itself. This means that it is important to make a high-quality dataset.

For this section, I have created a repository consisting of a collection of scripts used to create a NeRF dataset. It will use a program called COLMAP to infer the intrinsic and extrinsic parameters of the camera based on a set of images you give it.

However, before you start creating a dataset, here are some tips:

Here is an example of the trained output using a dataset that I created:

Happy Training!

References

[1] Mildenhall, B., Srinivasan, P. P., Tancik, M., Barron, J. T., Ramamoorthi, R., & Ng, R. (2021). Nerf: Representing scenes as neural radiance fields for view synthesis. Communications of the ACM, 65(1), 99-106.